DFS (Depth First Search) and BFS (Breadth First Search) Search Algorithms
In graph traversal, there are DFS (Depth First Search) and BFS (Breadth First Search). In this article, we will explore the concepts, differences, implementations, and real-world applications of these two algorithms.
1. DFS (Depth First Search)
DFS is an algorithm that explores as far as possible along each branch before backtracking. It’s similar to exploring a maze by going down one path until you can’t go any further, then backtracking and trying a different path. DFS can be implemented using recursion or a stack data structure.
How DFS Works:
- Start at the starting node and move as far as possible along each branch.
- When you reach a node with no unvisited adjacent nodes, backtrack to the previous node.
- Repeat this process until all nodes have been visited.
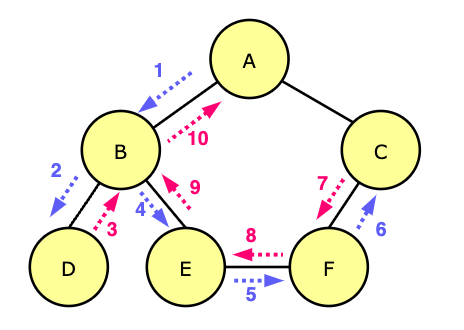
In the above diagram, the result of DFS is A, B, D, E, F, C.
DFS Implementation (Python Example):
def dfs(graph, start, visited=None):
if visited is None:
visited = set()
visited.add(start)
print(start, end=' ')
for neighbor in graph[start]:
if neighbor not in visited:
dfs(graph, neighbor, visited)
graph = {
'A': ['B', 'C'],
'B': ['D', 'E'],
'C': ['F'],
'D': [],
'E': ['F'],
'F': []
}
dfs(graph, 'A')
Output:
A B D E F C
Characteristics of DFS:
- Memory Efficiency: Uses a stack, so it requires less memory relative to the number of nodes.
- Depth-First: Explores nodes farthest from the starting point first, which is advantageous when deep paths are preferred.
- Usage in Tree Structures: DFS is often used for traversals (preorder, inorder, postorder) in binary trees.
Real-World Applications of DFS:
- Maze Solving: DFS is useful for exploring mazes since it goes down one path entirely before trying another.
- Finding Strongly Connected Components: Used in graphs to find strongly connected components.
- Backtracking Problems: Problems like the N-Queens problem are implemented based on DFS.
2. BFS (Breadth First Search)
BFS, in contrast to DFS, explores all neighbors at the present depth prior to moving on to nodes at the next depth level. It starts from the starting node and explores all its neighboring nodes first. BFS uses a queue data structure and is often used in finding the shortest path in unweighted graphs.
How BFS Works:
- Start from the starting node, enqueue all its adjacent nodes, and visit them.
- For each visited node, enqueue its adjacent unvisited nodes.
- Continue this process until all nodes are visited.
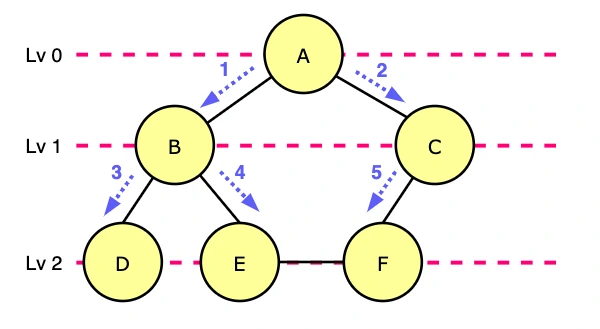
In the above diagram, the result of BFS is A, B, C, D, E, F.
BFS Implementation (Python Example):
from collections import deque
def bfs(graph, start):
visited = set()
queue = deque([start])
visited.add(start)
while queue:
vertex = queue.popleft()
print(vertex, end=' ')
for neighbor in graph[vertex]:
if neighbor not in visited:
queue.append(neighbor)
visited.add(neighbor)
graph = {
'A': ['B', 'C'],
'B': ['D', 'E'],
'C': ['F'],
'D': [],
'E': ['F'],
'F': []
}
bfs(graph, 'A')
Output:
A B C D E F
Characteristics of BFS:
- Shortest Path Search: Unlike DFS, BFS is advantageous for finding the shortest path. In unweighted graphs, it guarantees the shortest path from the starting node to any other node.
- Memory Usage: May use more memory as it stores all neighbors in the queue.
- Parallel Expansion: Since it explores nodes in order of proximity from the starting point, it can explore nodes at a certain depth all at once.
Real-World Applications of BFS:
- Shortest Path Finding: Used to find the shortest path between two points in structures like subway maps.
- Network Exploration: Commonly used to find paths between users in networks or social networks.
- Web Crawling: Used in search engines to traverse web pages by following link structures.
DFS vs. BFS: When to Use Which?
Let’s summarize the differences between these two algorithms.
| Category | DFS | BFS |
|---|---|---|
| Traversal Method | Explores as far as possible along each branch, uses recursion or stack | Explores neighbors level by level, uses queue |
| Data Structure | Stack (recursive calls) | Queue |
| Memory Usage | Less memory usage | More memory usage |
| Path Finding | Prefers deeper paths, doesn’t guarantee shortest path | Advantageous for shortest path search |
| Usage | Maze solving, backtracking problems | Shortest path finding, network exploration |
Conclusion
DFS and BFS are the two most fundamental algorithms in graph traversal. DFS explores nodes in depth-first order, making it advantageous for solving problems that require backtracking, while BFS explores nodes in breadth-first order, making it suitable for finding the shortest path. Deciding which traversal algorithm to use depends on the nature of the problem. By thoroughly understanding each algorithm and developing the ability to apply them to various problems, you can efficiently solve complex graph-related challenges.
