DFS(Depth First Search)와 BFS(Breadth First Search) 탐색 알고리즘

그래프 순회에는 DFS(Depth First Search, 깊이 우선 탐색)와 BFS(Breadth First Search, 너비 우선 탐색)가 있습니다.
이 글에서는 이 두 알고리즘의 개념, 차이점, 구현 그리고 실제 적용 사례를 알아보겠습니다.

1. DFS (깊이 우선 탐색)

DFS는 그래프나 트리의 깊은 부분부터 먼저 탐색하는 알고리즘입니다. 마치 미로를 탐험할 때 하나의 길을 끝까지 가보고 막히면 돌아와서 다른 길을 찾아가는 방식과 유사합니다. DFS는 재귀 호출이나 스택 자료구조를 사용하여 구현할 수 있습니다.

DFS 작동 원리:

탐색 시작점에서 시작하여 한 방향으로 갈 수 있는 끝까지 이동합니다.
더 이상 갈 수 없으면 이전 정점으로 돌아와서 아직 방문하지 않은 경로를 탐색합니다.
모든 경로를 탐색할 때까지 이 과정을 반복합니다.

DFS

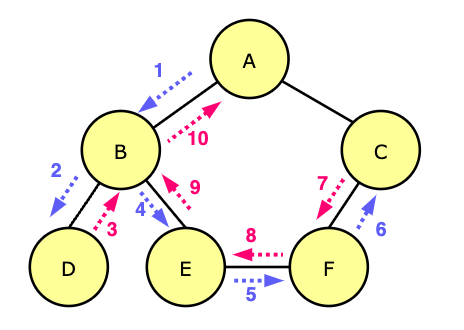
위 그림에서 DFS 결과는 A, B, D, E, F, C 입니다.

DFS 구현 (Python 예시):

def dfs(graph, start, visited=None):
    if visited is None:
        visited = set()
    visited.add(start)
    print(start, end=' ')
    
    for neighbor in graph[start]:
        if neighbor not in visited:
            dfs(graph, neighbor, visited)

graph = {
    'A': ['B', 'C'],
    'B': ['D', 'E'],
    'C': ['F'],
    'D': [],
    'E': ['F'],
    'F': []
}
dfs(graph, 'A')

출력:

A B D E F C

DFS의 특징:

메모리 효율성: 스택을 이용하기 때문에 노드 수에 비해 메모리 사용이 적습니다.
깊이 우선: 시작점에서 멀리 떨어진 노드를 먼저 탐색하므로, 길이 긴 경로를 선호할 때 유리합니다.
트리 구조에서의 용도: DFS는 이진 트리의 순회(전위, 중위, 후위)에 자주 사용됩니다.

DFS의 실제 적용 사례:

미로 찾기: DFS는 한 경로를 끝까지 탐색한 후 다른 경로를 시도하기 때문에 미로를 탐색하는 데 유용합니다.
강한 연결 요소 찾기: 그래프에서 강하게 연결된 컴포넌트를 찾을 때도 DFS가 사용됩니다.
백트래킹 문제: 예를 들어, N-퀸 문제와 같은 백트래킹 문제는 DFS를 기반으로 구현됩니다.

2. BFS (너비 우선 탐색)

BFS는 DFS와 반대로 너비를 우선으로 탐색하는 알고리즘입니다. 시작점에서 가까운 정점들부터 차례대로 탐색하는 방식입니다. BFS는 큐(Queue) 자료구조를 사용하여 구현되며, 최단 경로를 찾는 문제에 자주 사용됩니다.

BFS 작동 원리:

탐색 시작점에서 출발하여, 인접한 모든 정점을 큐에 넣고 방문합니다.
방문한 정점의 인접한 정점들을 다시 큐에 넣으며 너비를 넓혀갑니다.
모든 정점을 탐색할 때까지 이 과정을 반복합니다.

BFS

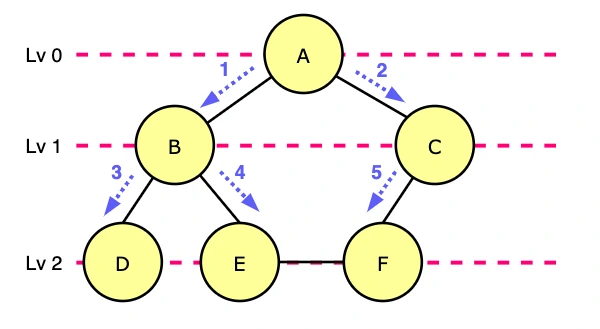
위 그림에서 BFS 결과는 A, B, C, D, E, F 입니다.

BFS 구현 (Python 예시):

from collections import deque

def bfs(graph, start):
    visited = set()
    queue = deque([start])
    visited.add(start)
    
    while queue:
        vertex = queue.popleft()
        print(vertex, end=' ')
        
        for neighbor in graph[vertex]:
            if neighbor not in visited:
                queue.append(neighbor)
                visited.add(neighbor)

graph = {
    'A': ['B', 'C'],
    'B': ['D', 'E'],
    'C': ['F'],
    'D': [],
    'E': ['F'],
    'F': []
}
bfs(graph, 'A')

출력:

A B C D E F

BFS의 특징:

최단 경로 탐색: DFS와 달리 BFS는 최단 경로 탐색에 유리합니다. 특히, 무가중치 그래프에서는 출발점에서 특정 정점까지의 최단 경로를 보장합니다.
메모리 사용: 큐에 모든 이웃을 저장하기 때문에 메모리 사용량이 많을 수 있습니다.
평행적 확장: 출발점에서 가까운 정점부터 차례대로 탐색하기 때문에 일정한 깊이에서의 노드를 한 번에 탐색할 수 있습니다.

BFS의 실제 적용 사례:

최단 경로 탐색: 지하철 노선도와 같은 그래프 구조에서 두 역 간의 최단 경로를 찾는 데 사용됩니다.
네트워크 탐색: BFS는 네트워크나 소셜 네트워크에서 특정 사용자로부터 다른 사용자까지 도달하는 경로를 찾는 데 자주 활용됩니다.
웹 크롤링: BFS는 검색 엔진에서 페이지 간의 링크 구조를 따라가며 웹을 탐색하는 데 사용됩니다.

DFS vs BFS: 어떤 상황에서 사용할까?

이제 두 알고리즘의 차이점을 요약해보겠습니다.

구분	DFS	BFS
탐색 방식	한 경로를 끝까지 탐색, 재귀적으로 탐색	가까운 노드부터 차례로 탐색, 큐 사용
자료구조	스택(재귀 호출) 사용	큐 사용
메모리	메모리 사용 적음	메모리 사용 많음
경로 탐색	깊은 경로 선호, 최단 경로 보장하지 않음	최단 경로 탐색에 유리
용도	미로 찾기, 백트래킹 문제	최단 경로 탐색, 네트워크 탐색

마무리

DFS와 BFS는 그래프 탐색에서 가장 중요한 두 가지 알고리즘입니다.
DFS는 깊이를 먼저 탐색하는 방식으로 백트래킹과 같은 문제 해결에 유리하며, BFS는 너비를 우선으로 탐색하여 최단 경로를 찾는 데 적합합니다.
문제의 성격에 따라 어떤 탐색 알고리즘을 사용할지 결정하는 것이 중요합니다.
각 알고리즘을 정확히 이해하고, 다양한 문제에서 응용할 수 있는 능력을 기른다면, 복잡한 그래프 문제도 효율적으로 해결할 수 있습니다.

dev-yyh

Contact