이진 트리 (Binary tree) 알아보기

이진 트리는 컴퓨터 과학에서 가장 기본적이고 중요한 데이터 구조 중 하나입니다. 이 글에서는 이진 트리의 개념, 유형, 속성, 표현 방법 및 응용 분야에 대해 알아보겠습니다.

이진 트리(Binary tree) 란?

이진 트리(Binary Tree)는 각 노드가 최대 두 개의 자식 노드를 갖는 계층적 데이터 구조입니다. 이러한 구조는 데이터의 효율적인 저장, 검색 및 관리를 가능하게 합니다.

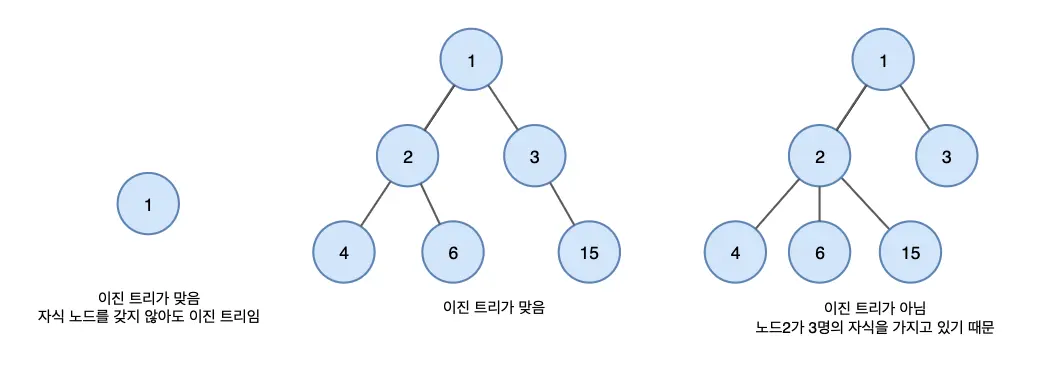
이진트리 유형

1. 전 이진 트리 (Full Binary Tree or Strict Binary Tree)

전 이진 트리는 모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리입니다. 즉, 각 노드는 자식이 없거나 두 개의 자식을 반드시 갖습니다.

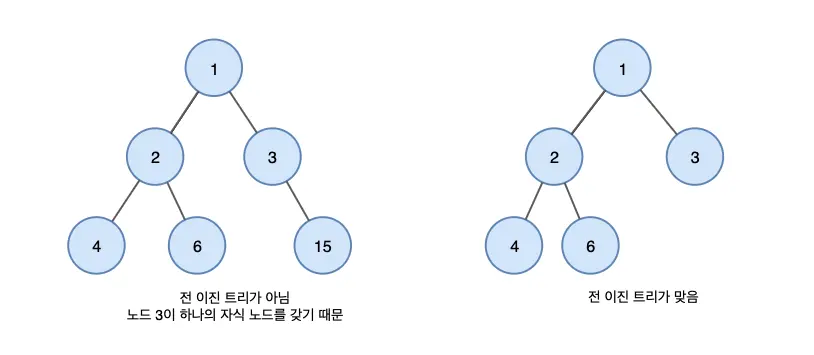
2. 완전 이진 트리 (Complete Binary Tree)

완전 이진 트리는 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있는 트리입니다.
마지막 레벨은 꽉 차 있지 않아도 되지만 노드가 왼쪽에서 오른쪽으로 채워져야 합니다.

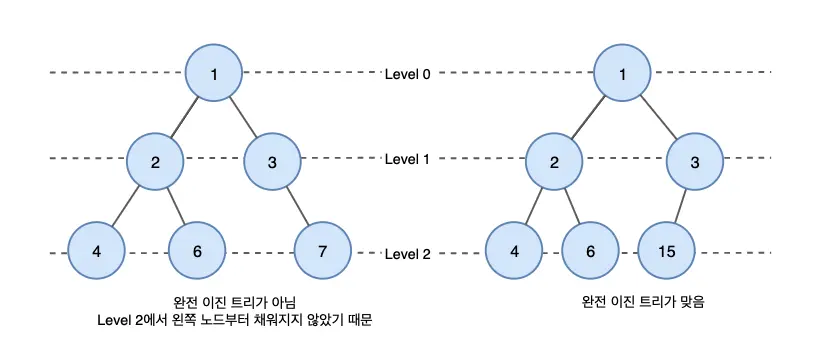
포화 이진 트리 (Perfect Binary Tree)

포화 이진 트리는 모든 내부 노드가 정확히 두 개의 자식 노드를 가지며, 모든 리프 노드가 동일한 깊이 또는 레벨을 갖습니다.

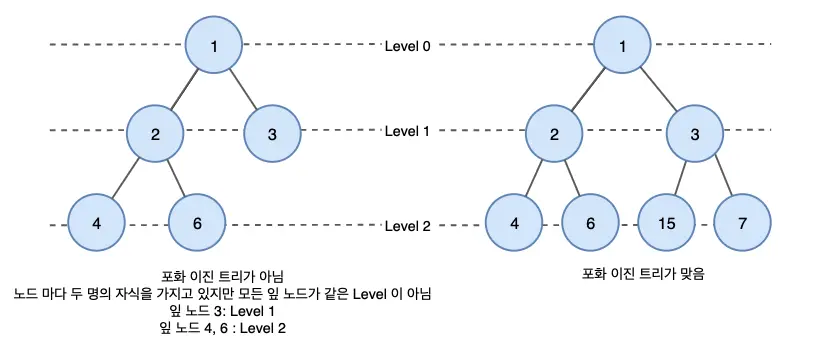
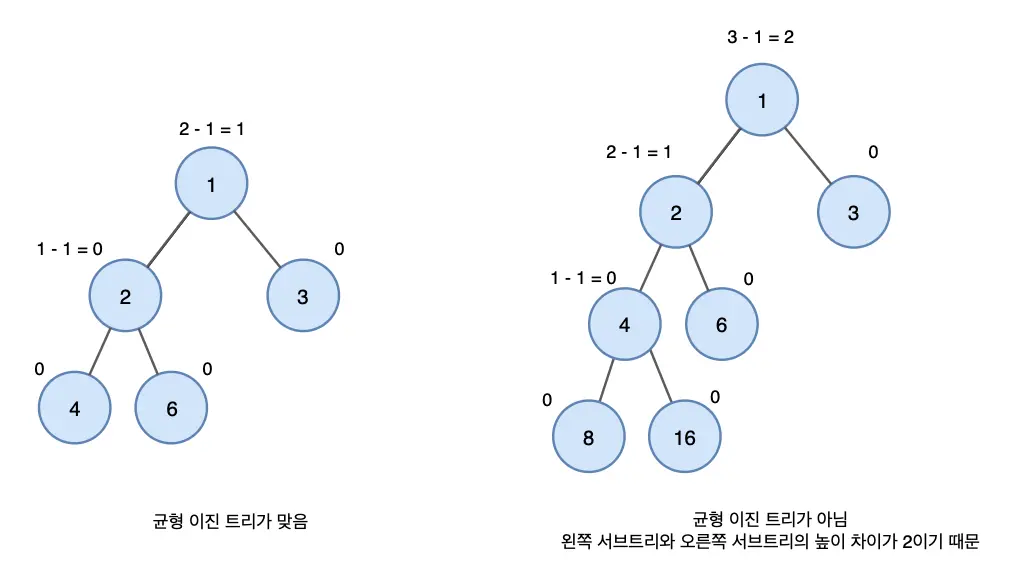
균형 이진 트리 (Balanced Binary Tree)

균형 이진 트리는 모든 노드에 대해 왼쪽 및 오른쪽 부분 트리의 높이 차이가 최대 1인 트리입니다. AVL 트리와 레드-블랙 트리가 대표적인 예입니다.

이진 트리 속성

이진 트리는 다음과 같은 속성이 있습니다.

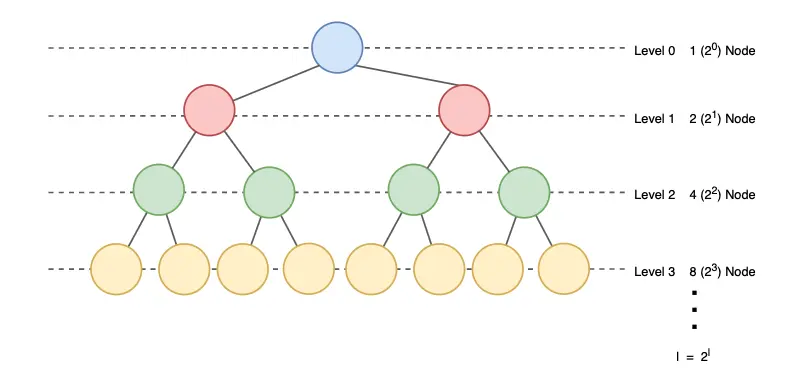
1. 이진 트리의 레벨 l에서 노드의 최대 수는 \(2^l\) 입니다.

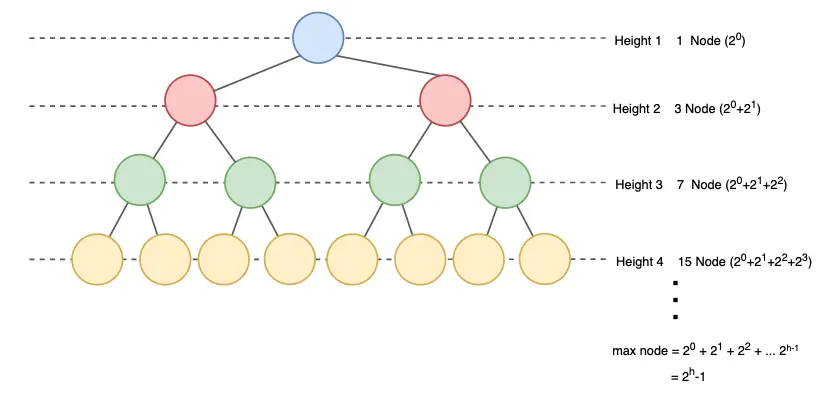
2. 높이가 h이고 하나의 노드를 가진 트리의 높이가 1이라면 최대 노드 수는 \(2^h - 1\)이고 높이가 0이라면 \(2^{h+1} - 1\)입니다.

3. 잎 노드 높이가 1이라면 최소 높이는 \(log_2(N+1)\)입니다. 잎 노드의 높이가 0이라면 \(log_2(N+1) - 1\)입니다.

\(2^h - 1 = n\)
\(2^h = n + 1\)
\(log_2(2^h) = log_2(n + 1)\)
\(h = log_2(n + 1)\)

4. 전 이진트리에서 리프 노드 수는 항상 자식이 두 개인 노드보다 하나 더 많습니다.

L = 리프 노드 수
T = 두 명의 자식을 가진 internal node 수
L = T + 1

이진 트리의 표현 방법

이진 트리는 배열 또는 연결 리스트를 통해 구현할 수 있습니다.

1. 배열(순차적) 표현

배열을 사용하여 이진 트리를 표현하면 노드의 인덱스를 기반으로 부모와 자식 노드 간의 관계를 쉽게 파악할 수 있습니다.

루트 노드의 인덱스 i가 0인 경우

• 노드 i에 왼쪽 자식은 2*i+1 번째 노드이다.
• 노드 i에 오른쪽 자식은 2*i+2 번째 노드이다.
• 노드 i에 부모는 (i-1)/2 번째 노드이다.

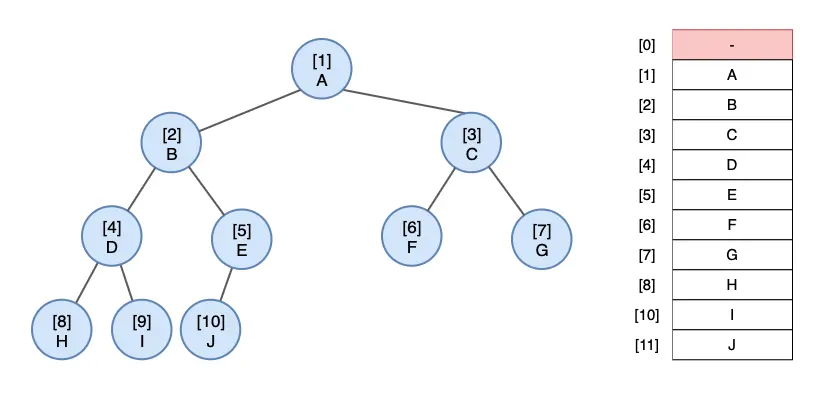
루트 노드의 인덱스 i가 1인 경우

• 노드 i에 왼쪽 자식은 2*i 번째 노드이다.
• 노드 i에 오른쪽 자식은 2*i+1 번째 노드이다.
• 노드 i에 부모는 i/2 번째 노드이다.

배열로 표현한 완전이진트리 - 배열 공간을 효율적으로 쓰고 있습니다.

편향 트리(skew tree) 인 경우 - 많은 공간이 낭비되고 있습니다.

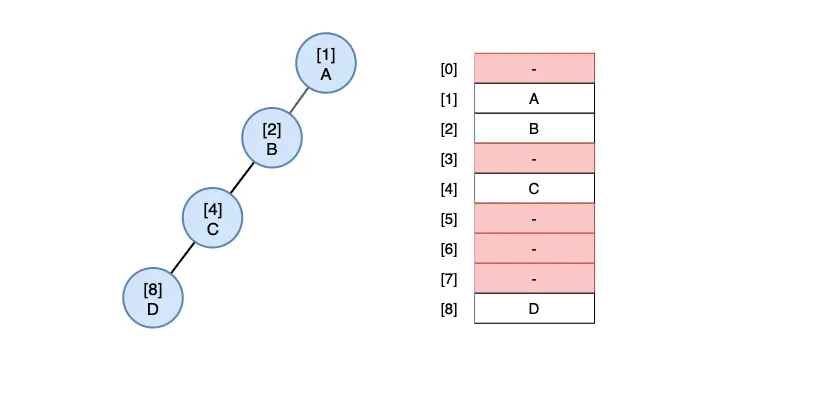
배열 표현의 장단점

• 장점: 노드 접근 속도가 빠르고 구현이 간단합니다.
• 단점: 편향 트리에서는 메모리 낭비가 발생하며, 배열 크기에 제한이 있어 노드 추가에 제약이 있습니다.

2. 연결 리스트 표현

포인터를 사용하여 각 노드가 자신의 자식 노드를 가리키도록 연결 리스트 형태로 구현할 수 있습니다.

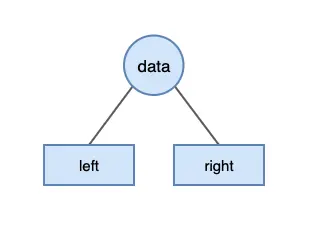
C 언어에서 정수를 저장하는 이진 트리 노드는 다음과 같이 정의할 수 있습니다.

struct BinaryTreeNode {
  int data;
  struct BinaryTreeNode *left
  struct BinaryTreeNode *right
}

연결 리스트 표현의 장단점

• 장점: 노드 수에 제한이 없으며, 삽입과 삭제가 용이합니다.
• 단점: 배열에 비해 노드 접근 속도가 느립니다.

이진 트리의 응용 분야

이진 트리는 다양한 분야에서 중요한 역할을 합니다.

1. 수식 트리(Expression Tree): 수학적 표현식을 트리 형태로 나타내어 계산 순서를 정의합니다.
2. 허프만 코딩 트리(Huffman Coding Tree): 데이터 압축 알고리즘에서 문자별 빈도를 기반으로 최적의 이진 트리를 생성합니다.
3. 이진 검색 트리(Binary Search Tree, BST): 효율적인 검색, 삽입, 삭제를 지원하는 트리 구조입니다.
4. 우선순위 큐(Priority Queue): 힙(Heap) 자료 구조를 사용하여 우선순위에 따라 요소를 관리합니다.