트리 순회 (Tree Traversal): 전위, 중위, 후위, 그리고 레벨 순회

트리 순회는 노드를 특정한 순서대로 방문하는 방법으로, 각각의 방식은 다양한 문제 해결에 응용될 수 있습니다. 이번 글에서는 트리 순회 방법 네 가지인 전위 순회(Pre-order), 중위 순회(In-order), 후위 순회(Post-order), 그리고 레벨 순회(Level-order)에 대해 알아보겠습니다.

트리 순회(Tree Traversal)란?

트리 순회(Tree Traversal)는 트리 구조 내의 모든 노드를 체계적이고 한 번씩만 방문하는 과정을 말합니다. 이는 트리의 데이터를 처리하거나 특정 조건의 노드를 찾는 등 다양한 작업에서 기본이 되는 과정입니다.

트리 순회의 주요 목적은 다음과 같습니다.

데이터 처리: 각 노드의 데이터를 읽거나 수정합니다.
검색: 특정 값을 찾거나 조건에 맞는 노드를 탐색합니다.
복사 및 변환: 트리를 복제하거나 다른 구조로 변환합니다.

트리 순회 방법은 다음과 같습니다.

전위 순회(Pre-order Traversal)
중위 순회(In-order Traversal)
후위 순회(Post-order Traversal)
레벨 순회(Level-order Traversal)

1. 전위 순회 (Pre-order Traversal)

전위 순회는 루트 노드를 가장 먼저 방문하고, 그 다음에 왼쪽 자식을 방문한 후 오른쪽 자식을 방문하는 방식입니다. 트리의 구조를 출력하거나 복제할 때 유용하게 사용됩니다.

전위 순회의 순서:

루트 노드를 방문한다.
왼쪽 서브트리를 전위 순회한다.
오른쪽 서브트리를 전위 순회한다.

Pre-order Traversal

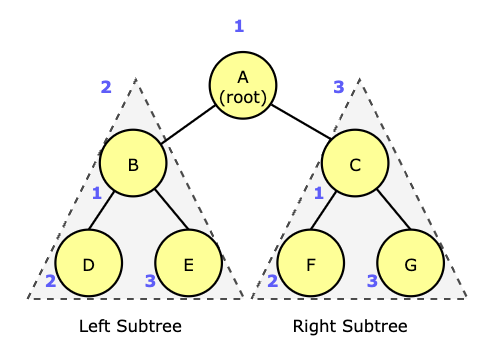
위 그림에서 전위 순회 결과는 A, B, D, E, C, F, G 입니다.

전위 순회 알고리즘 (재귀):

def pre_order(node):
    if node:
        print(node.value, end=' ')  # 루트 방문
        pre_order(node.left)        # 왼쪽 서브트리 방문
        pre_order(node.right)       # 오른쪽 서브트리 방문

전위 순회의 특징:

루트를 가장 먼저 방문하기 때문에, 트리의 구조를 복제하거나 표현식을 전위 표기법으로 변환할 때 유용합니다.
파일 시스템에서 디렉터리 구조를 탐색할 때 유용하게 사용됩니다.

2. 중위 순회 (In-order Traversal)

중위 순회는 왼쪽 자식을 먼저 방문한 후 루트 노드를 방문하고, 그 다음 오른쪽 자식을 방문하는 방식입니다. 이 방법은 이진 탐색 트리에서 매우 중요한 역할을 하며, 노드들을 오름차순으로 정렬하는 데 사용할 수 있습니다.

중위 순회의 순서:

왼쪽 서브트리를 중위 순회한다.
루트 노드를 방문한다.
오른쪽 서브트리를 중위 순회한다.

In-order Traversal

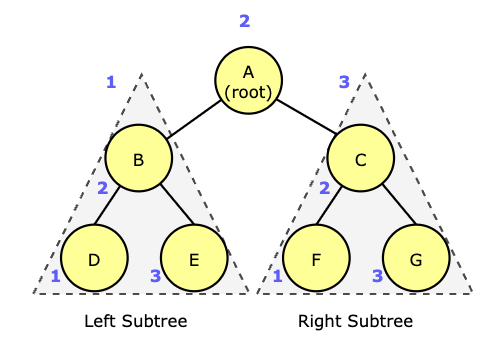
위 그림에서 중위 순회 결과는 D, B, E, A, F, C, G 입니다.

중위 순회 알고리즘 (재귀):

def in_order(node):
    if node:
        in_order(node.left)         # 왼쪽 서브트리 방문
        print(node.value, end=' ')  # 루트 방문
        in_order(node.right)        # 오른쪽 서브트리 방문

중위 순회의 특징:

이진 탐색 트리에서 중위 순회를 사용하면 값이 정렬된 순서로 출력됩니다.
트리 구조를 순서대로 출력하거나 정렬된 데이터를 얻고자 할 때 많이 사용됩니다.

3. 후위 순회 (Post-order Traversal)

후위 순회는 왼쪽 자식과 오른쪽 자식을 먼저 모두 방문한 후에 루트 노드를 마지막에 방문하는 방식입니다. 이 방식은 트리의 자식 노드를 먼저 모두 처리한 후 부모 노드를 처리하는 문제에서 유용하게 사용됩니다.

후위 순회의 순서:

왼쪽 서브트리를 후위 순회한다.
오른쪽 서브트리를 후위 순회한다.
루트 노드를 방문한다.

Post-order Traversal

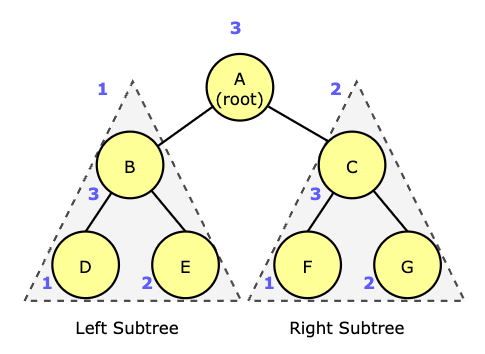
위 그림에서 후위 순회 결과는 D, E, B, F, G, C, A 입니다.

후위 순회 알고리즘 (재귀):

def post_order(node):
    if node:
        post_order(node.left)       # 왼쪽 서브트리 방문
        post_order(node.right)      # 오른쪽 서브트리 방문
        print(node.value, end=' ')  # 루트 방문

후위 순회의 특징:

자식 노드를 모두 처리한 후 부모 노드를 처리하는 방식이기 때문에, 트리 구조의 삭제나 메모리 해제와 같은 작업에 적합합니다.
컴퓨터 시스템에서 디렉토리 구조를 삭제할 때 자주 사용됩니다.

4. 레벨 순회 (Level-order Traversal)

레벨 순회는 앞의 순회 방식들과 달리 트리의 높이별로 노드를 순차적으로 방문하는 방식입니다. 가장 높은 레벨의 루트 노드부터 시작하여 한 레벨씩 내려가며 모든 노드를 방문합니다. 이 방식은 너비 우선 탐색(BFS) 방식으로 구현됩니다.

레벨 순회의 순서:

루트 노드를 방문한다.
그 다음 레벨의 노드를 왼쪽에서 오른쪽 순서로 방문한다.
이 과정을 모든 레벨에 대해 반복한다.

Level-order Traversal

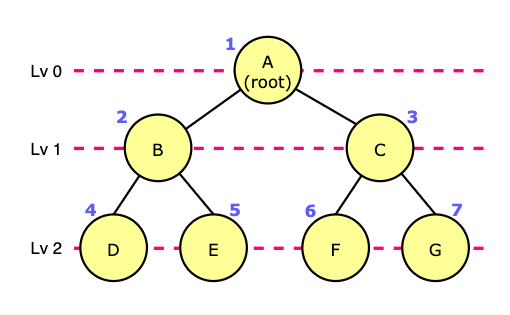
위 그림에서 레벨 순회 결과는 A, B, C, D, E, F, G 입니다.

레벨 순회 알고리즘 (큐를 이용한 구현):

from collections import deque

def level_order(node):
    if not node:
        return
    queue = deque([node])
    while queue:
        current = queue.popleft()
        print(current.value, end=' ')
        if current.left:
            queue.append(current.left)
        if current.right:
            queue.append(current.right)

레벨 순회의 특징:

트리의 높이에 따라 노드를 방문하기 때문에, 최단 경로 탐색과 같은 문제 해결에 적합합니다.
이진 힙(binary heap)과 같은 자료구조에서 사용되며, 노드의 너비를 기준으로 처리해야 할 때 유용합니다.

트리 순회 방식의 비교

순회 방식	순서	특징	주요 용도
전위 순회	루트 → 왼쪽 자식 → 오른쪽 자식	루트 노드를 먼저 방문하는 방식	트리 구조 복사, 재귀적 문제 해결
중위 순회	왼쪽 자식 → 루트 → 오른쪽 자식	이진 탐색 트리에서 정렬된 순서로 방문	이진 탐색 트리에서 값 정렬
후위 순회	왼쪽 자식 → 오른쪽 자식 → 루트	자식 노드를 먼저 방문한 후 부모 노드를 처리	트리 삭제, 메모리 해제
레벨 순회	높이별로 왼쪽에서 오른쪽으로 방문	너비 우선 탐색, 큐를 사용하여 구현	최단 경로 탐색, 넓이 기반 탐색

마무리

트리 순회는 트리 자료구조에서 각 노드를 탐색하는 중요한 방법입니다.
각 순회 방법은 특정 상황에서 유리한 특성을 가지므로, 문제의 특성과 해결하려는 방식에 맞춰 적절한 순회 방법을 선택하는 것이 중요합니다.
전위, 중위, 후위, 그리고 레벨 순회의 개념을 명확히 이해하고 활용하면, 다양한 트리 기반 문제를 효율적으로 해결할 수 있을 것입니다.

dev-yyh

Contact